Interpolations: All Flows are One Flow

Various interpolation schemes have been suggested in different methods. How do they impact performance? Is the simplest straight-line interpolation enough?

Most diffusion and flow models can be analyzed through the rectified flow lens, but they employ different interpolation methods, typically affine interpolations such as straight-line or spherical interpolations. A critical question is to understand the impact of using different interpolation processes. This blog introduces the equivalent relationships between rectified flows induced by these different interpolation processes, as discussed in Chapter 3 of these lecture notes. Related observations and discussions can also be found in .

Overview

Given a coupling $(X_0, X_1)$ of the noise $X_0 \sim \pi_0$ and data $X_1 \sim \pi_1$, in rectified flow, we leverage an interpolation process $X_t = \mathtt{I}_t(X_0, X_1)$, $t \in [0,1]$, to smoothly connect $X_0$ and $X_1$, and then “causalize” or “rectify” the interpolation $\{X_t\}$ into its rectified flow $\{Z_t\} = \mathtt{Rectify}(\{X_t\})$, an ODE-based generative model of the form:

\[\mathrm{d}Z_t = v_t(Z_t) \mathrm{d}t, \quad Z_0 = X_0, \quad \text{with velocity field} \quad v_t(x) = \mathbb{E}[\dot{X}_t \mid X_t = x],\]

where $\dot{X}_t$ is the time derivative of $X_t$. This formulation of $v_t$ ensures that $Z_t$ matches in distribution with $X_t$ at every time $t$. With this, we can generate data as $Z_1$ by evolving forward in time from noise $Z_0$. Intuitively, the rectified flow $\{Z_t\}$ “rewires” the trajectories of $\{X_t\}$ at their intersection points to produce non-intersecting ODE trajectories. For further details, see paper, blog, blog.

In principle, any time-differentiable interpolation process $\{X_t\}$ that connects $X_0$ and $X_1$ can be used within this framework. Different methods employ different interpolation schemes. The simplest choice is the straight-line interpolation, defined as

\[X_t = t X_1 + (1-t) X_0,\]

which is naturally justified by optimal transport theory.

Alternatively, other methods, such as DDIM and probability-flow ODEs, use curved interpolation schemes of a more general affine form:

\[X_t = \alpha_t X_1 + \beta_t X_0,\]

where $\alpha_t$ and $\beta_t$ are chosen in different ways depending on the method.

Questions: What is the impact of the choice of interpolation? Do different interpolation schemes yield fundamentally different rectified flow dynamics?

At first glance, it may appear that the interpolation process must be chosen during the training phase, as it directly affects the learned rectified flow. However, this is not necessarily the case.

As it turns out, if two interpolation processes can be deformed into each other with a differentiable pointwise transform (i.e., they are diffeomorphic in mathy terms), then the trajectories of their rectified flows can also be deformed into each other using the very same transform. In addition, if the two processes are constructed from the same couplings, then their rectified flows lead to the same rectified coupling $(Z_0, Z_1).$

Why is this true? The intuition is illustrated in Figure 1. The trajectories of the rectified flow (RF) are simply a “rewiring” of the interpolation trajectories at their intersection points to avoid crossings. As a result, they occupy the same “trace” as the interpolation process, even though they switch between different trajectories at intersection points. Consequently, any deformation applied to the interpolation trajectories is inherited by the rectified flow trajectories. The deformation must be point-to-point here to make it insenstive to the rewiring of the trajectories.

This is a general and fundamental property of the rectification process and is not restricted to specific distributions, couplings, or interpolations.

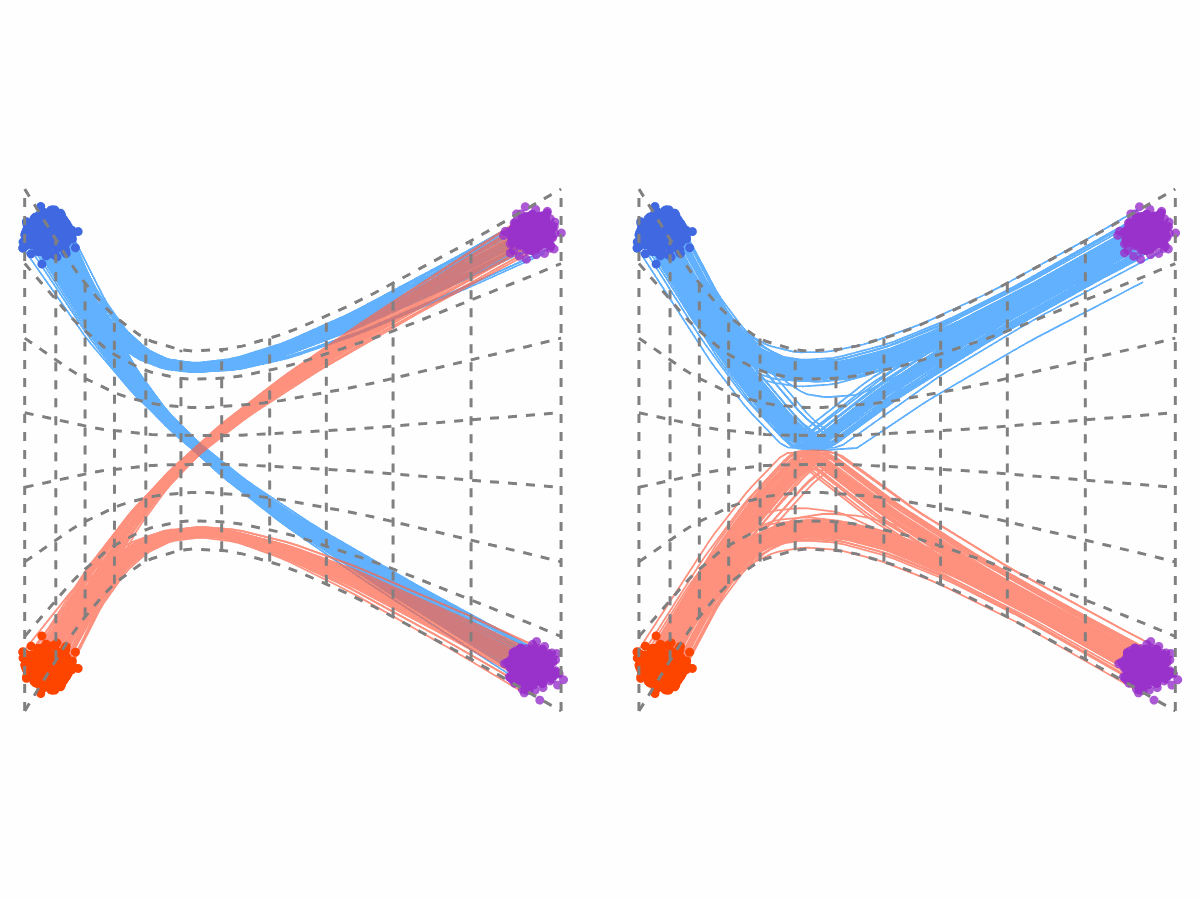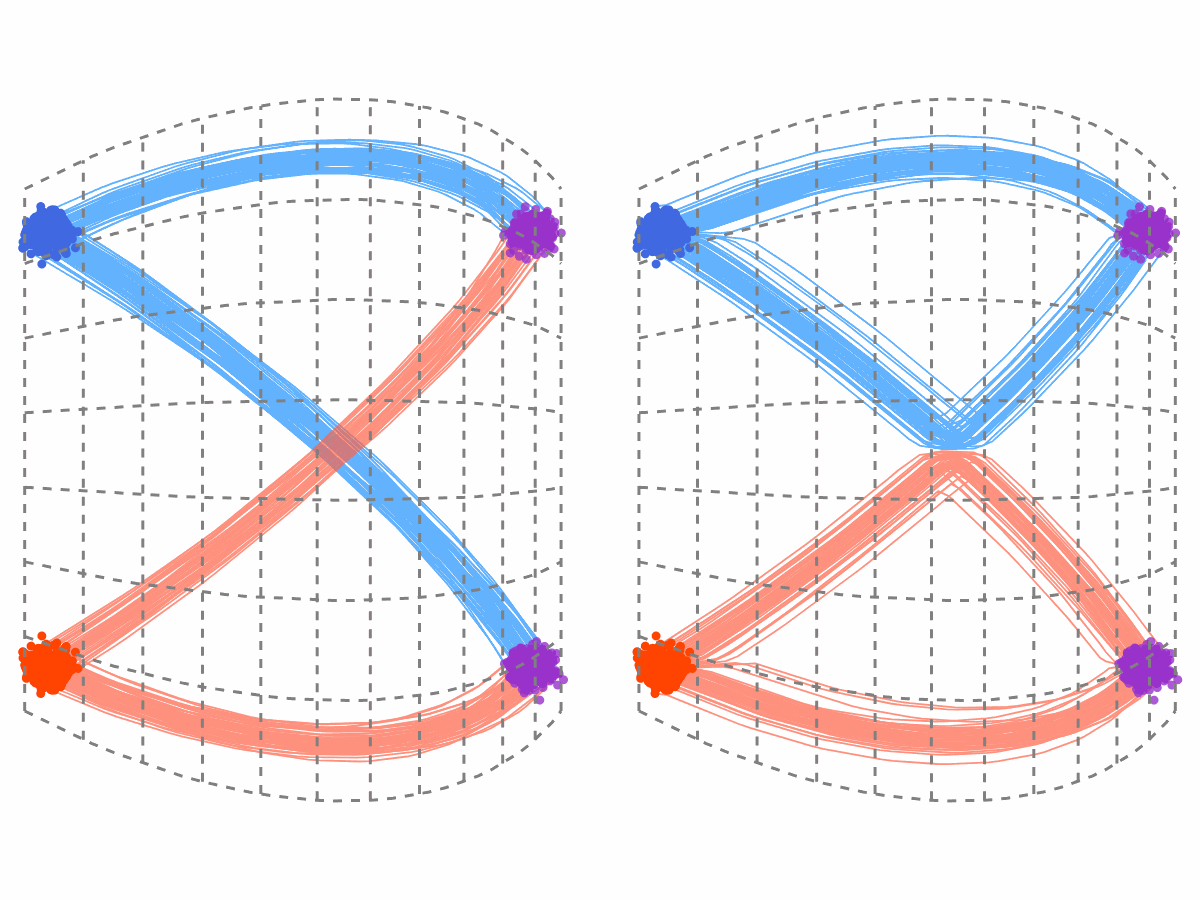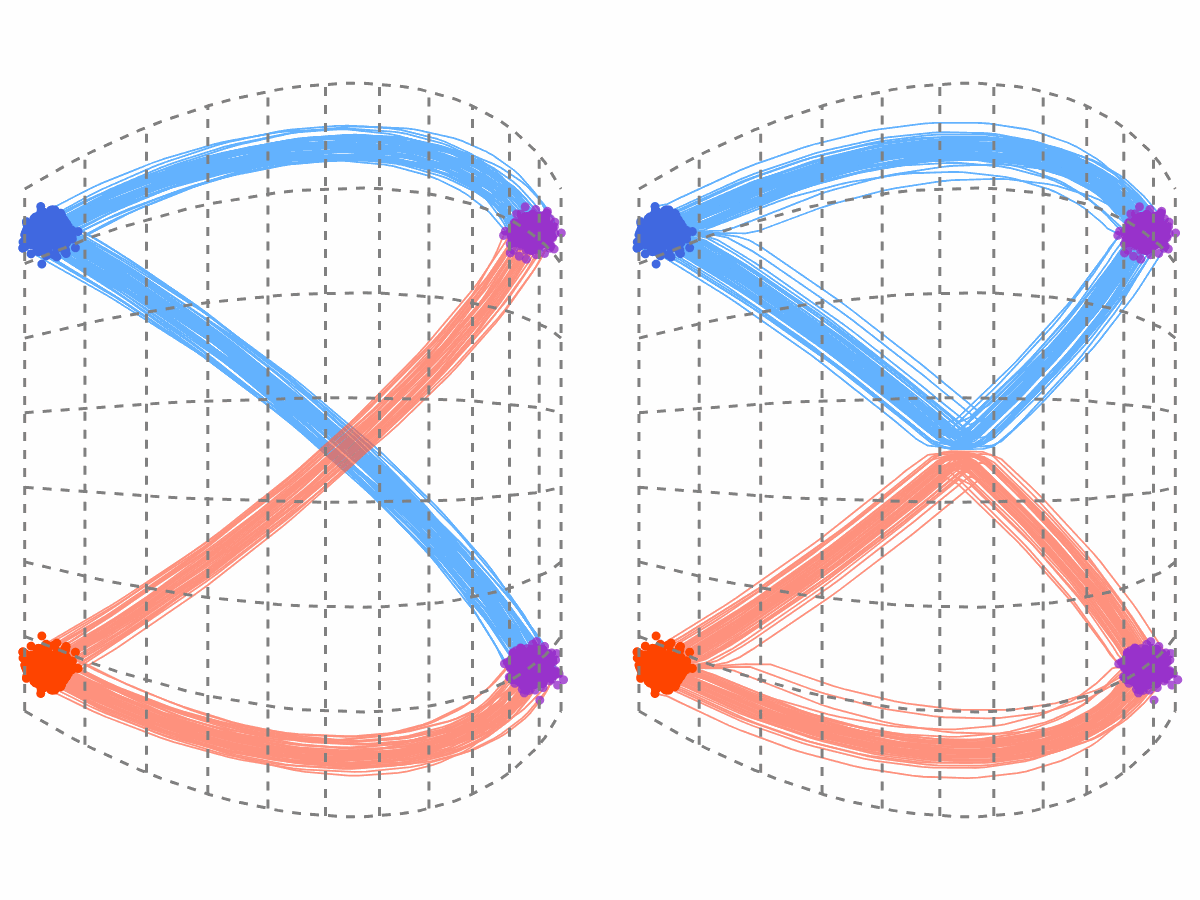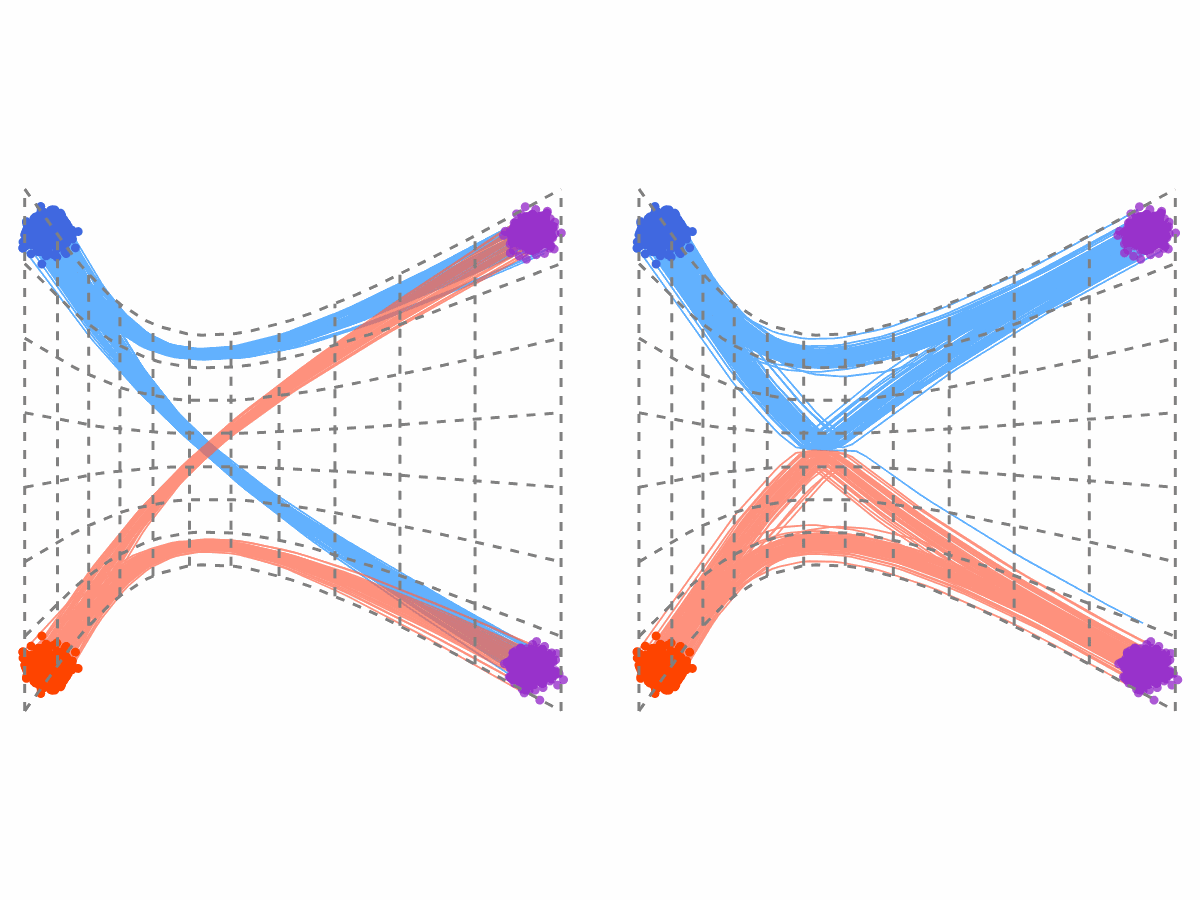
interpolation conversion gif — Figure 1. Rectified flow (right) rewires the interpolation trajectories (left) to avoid crossing. When a deformation is applied on the interpolation trajectories, the trajectories of the corresponding rectified flow is deformed in the same way.

Notably, all affine interpolation processes $X_t = \alpha_t X_1 + \beta_t X_0$ can be pointwisely transformed into one another through simple time and variable scaling. This suggests that, in principle, it is sufficient to use the simplest straight-line interpolation during training, while recovering the rectified flow for all affine interpolations at inference time.

This analytic relation allows us to analyze the impact of training and inference under different interpolations. For training, using different affine interpolations corresponds to applying time weightings in the training loss. We analyze this for the common straight-line and cosine interpolations and find that it appears to have limited impact on performance. For inference, using different interpolations corresponds to applying numerical discretization on deformed ODE trajectories, which is discussed in depth in this blog.

Point-wisely Transformable Interpolations

We first formalize pointwise transformability between two interpolation processes.

Definition 1. Let $\{X_t : t \in [0,1]\}$ and $\{X'_t : t \in [0,1]\}$ be two interpolations. They are pointwise transformable if there exist differentiable maps
\[\tau: [0,1] \to [0,1] \quad \text{ and } \quad \phi: [0,1] \times \mathbb{R}^d \to \mathbb{R}^d\]
such that each $\phi_t$ is invertible, and
\[X'_t = \phi_t(X_{\tau_t}), \quad \forall t \in [0,1].\]

If two interpolations are contructed from the same coupling $(X_0, X_1)$ and are pointwise transformable, then their rectified flows are also related by the same transform, and also lead to the same rectified coupling.

Theorem 1. Suppose $\{X_t\}$ and $\{X'_t\}$ constructed from the same coupling $(X_0, X_1) = (X'_0, X'_1)$ and are pointwise transformable. Assume $\tau_0=0$ and $\tau_1=1$.

Let $\{Z_t\}$ and $\{Z'_t\}$ be their rectified flows:
\[\{Z_t\} = \mathtt{Rectify}(\{X_t\}),~~~~~~ \{Z_t\} = \mathtt{Rectify}(\{X_t\}).\]

$\{Z_t\},\{Z'_t\}$ can be transformed with the same pointwise maps:
\[Z'_t = \phi_t(Z_{\tau_t}) \quad \forall t \in [0,1].\]

Their rectified couplings are the same: $(Z_0, Z_1) = (Z'_0, Z'_1).$

Let $\{v_t\}$ and $\{v'_t\}$ be the velocity fields of the rectified flows $\{Z_t\}$ and $\{Z_t'\}$, respectively. We have
\[v'_t(x) = \partial_t \phi_t(\phi_t^{-1}(x)) + \bigl(\nabla \phi_t(\phi_t^{-1}(x))\bigr)^\top v_{\tau_t}(\phi_t^{-1}(x)) \dot{\tau}_t. \tag{1}\]

This is equivalent to saying that the $\{Z_t\} = \texttt{Rectify}(\{X_t\})$ map is equivariant under the pointwise transforms $\{X_t'\}=\texttt{Transform}(\{X_t\})$, while the the rectified coupling map $(Z_0,Z_1) = \mathtt{RectifyCoupling}(\{X_t\})$ is equivalent:

\[\texttt{Rectify}(\texttt{Transform}(\{X_t\})) = \texttt{Transform}(\texttt{Rectify}(\{X_t\})),\] \[\texttt{RectifyCoupling}(\texttt{Transform}(\{X_t\})) = \texttt{RectifyCoupling}(\{X_t\}).\]

Affine Interpolations are Pointwise Transformable

Many commonly used interpolation schemes are affine $X_t = \alpha_t X_1 + \beta_t X_0,$ with $\alpha_t$ and $\beta_t$ are monotone, $\alpha_0=\beta_1=0,$ and $\alpha_1 = \beta_0 = 1.$ Examples include:

Straight interpolation :
\[X_t = tX_1 + (1-t) X_0.\]
This yields straight lines connecting $\pi_0$ and $\pi_1$ at constant speed $\dot X_t = X_1 - X_0.$
Spherical linear interpolation (slerp) :
\[X_t = \sin\left(\frac{\pi}{2} t\right)X_1 + \cos\left(\frac{\pi}{2} t\right)X_0,\]
which traces a shortest great-circle arc on a sphere at constant speed.
DDPM/DDIM interpolation A spherical interpolation satisfying $\alpha_t^2 + \beta_t^2 = 1$ but with a non-uniform speed defined by $\alpha_t$:
\[X_t = \alpha_t X_1 + \sqrt{1-\alpha_t^2} X_0,\]
where $\alpha_t = \exp\bigl(-\frac{1}{4}a(1-t)^2 - \tfrac{1}{2}b(1-t)\bigr)$, and $a=19.9,b=0.1$ by default.

All affine interpolations are pointwise transformable by adjusting time and scaling. In this case, the maps $\phi$ and $\tau$ reduce to scalar transforms, as observed in a line of works . Hence, the rectified flows of all affine interpolations can be analytically transformed into one another, and they lead to the same rectified couplings.

Proposition 1. Pointwise Transforms Between Affine Interpolations

Let $X_t = \alpha_t X_1 + \beta_t X_0$ and $X_t' = \alpha_t' X_1 + \beta_t' X_0$ be two affine interpolations from the same coupling $(X_0, X_1).$ Then there exist scalar functions $\tau_t$ and $\omega_t$ such that
\[X_t' = \frac{1}{\omega_t} X_{\tau_t}, \quad \forall t \in [0,1], \tag{2}\]
where $\tau_t$ and $\omega_t$ solve
\[\frac{\alpha_{\tau_t}}{\beta_{\tau_t}} = \frac{\alpha'_t}{\beta'_t}, \quad \omega_t = \frac{\alpha_{\tau_t}}{\alpha'_t} = \frac{\beta_{\tau_t}}{\beta'_t}, \quad \forall t \in (0, 1)\]
with the boundary conditions $\omega_0 = \omega_1 = 1, \tau_0 = 0, \tau_1 = 1.$

In practice, we can determine $\tau_t$ numerically—e.g., via a binary search—or derive an analytic solution in certain simple cases.

Figure 2. The transforms $\tau$ and $\omega$ in Equation (2) that convert DDIM to spherical interpolation (left) and convert straight interpolation to spherical (right). When converting DDIM to spherical, $\omega_t$ remains fixed at 1, because only the time scaling changes.

Combining Proposition 1 with Theorem 1, we have:

Proposition 2. Rectified Flows between Affine Interpolations

For the affine interpolations $\{X_t\}$ and $\{X'_t\}$ in Proposition 1, we have

Their rectified flows $\{Z_t\}$ and $\{Z'_t\}$ satisfy:

\[Z'_t = \frac 1 {\omega_t} Z_{\tau_t}, \quad \forall t \in [0, 1].\]

Their rectified couplings are identical: $(Z_0, Z_1) = (Z'_0, Z'_1).$

Their rectified flow velocity fields $v_t$ and $v'_t$ relate via:

\[v'_t(x) = \frac{\dot{\tau}_t}{\omega_t} v_{\tau_t}(\omega_t x) - \frac{\dot{\omega}_t}{\omega_t} x. \tag{3}\]

Example 1. Velocity from Straight to Affine

Converting the straight interpolation $X_t=tX_1 + (1-t)X_0$ with $\alpha_t=t$ and $\beta_t=1-t$ into another affine interpolation $X'_t = \alpha'_t X_1 + \beta'_t X_0$ gives:
\[\tau_t = \frac{\alpha'_t}{\alpha'_t + \beta_t'}, \quad \omega_t = \frac{1}{\alpha_t' + \beta_t'}.\]
Their rectified flow velocity fields satisfy:
\[v'_t(x) = \frac{\dot{\alpha}'_t \beta'_t - \alpha'_t \dot{\beta}'_t}{\alpha'_t + \beta'_t} v_{\tau_t}(\omega_t x) \;+\; \frac{\dot{\alpha}'_t + \dot{\beta}'_t}{\alpha'_t + \beta'_t} x.\]

Figure 3. We first train a rectified flow using straight interpolation, and then transform it into the RF of spherical interpolation by applying the transformation formula described above. While the transformation results in different ODE trajectories, both ultimately converge to the same endpoints $Z_1$, as predicted by Proposition 2. The result is obtained by solving the ODE using 100 Euler steps.

Implication on Inference

The trajectories of the RF derived from different affine interpolations can be viewed as deformations of one another via time and space scaling. When the same numerical discretization methods, such as the Euler method, are applied to these differently deformed trajectories, they produce varying discretization errors, leading to numerically different estimations of $Z_1$ . This difference becomes pronounced when a large step size is used, as it introduces significant discretization errors; see Figure 4 for an example of the Euler method with 4 steps. However, the difference diminishes as the discretization becomes sufficiently fine to accurately approximate the underlying ODEs (as shown in Figure 3 with 100 Euler steps).

Figure 5 illustrates how the difference in the predicted outcome $Z_1$ of the RF ODEs corresponding to straight and spherical interpolation decreases as the number of Euler steps increases.

Figure 4. Different final generated samples when the number of Euler steps is reduced to 4.

Figure 5. The mean square error (MSE) between the estimtion of $Z_1$ from rectified flows induced from straight versus spherical interpolation decreases as the number of inference steps increases, reflecting their shared continuous-time limit. Nevertheless, different discretization schemes produce varying performance when the step count is small.

In general, we may want to reduce these errors by seeking “straighter” trajectories when the Euler method is used for discretization. Note, however, if “curved” variants of the Euler method are employed, the notion of straightness must be adapted to account for the curvature inherent in the curved Euler method. For further discussion, refer to this blog.

Although it is challenging to predict the best inference interpolation scheme a priori, the post-training conversion above allows us to choose whichever scheme that yields best sampling results in practice. Moreover, one can go a step further by directly optimizing the pointwise transform to minimize discretization error, without worrying about which interpolation scheme it corresponds to. Specifically, this involves directly finding the pair $(\phi_t, \tau_t)$ such that the Euler method applied to the transformed ODE, $Z_t' = \phi_t(Z_{\tau_t})$, is as accurate as possible.

Implications on Loss Functions

Suppose we have a parametric model $v_t(x;\theta)$ trained to approximate the RF velocity field $v_t(x)$ under a specific affine interpolation. After training, we can use the relationships derived above to convert this model into $v'_t(x;\theta)$, corresponding to a different affine interpolation, without retraining. Some questions arise:

How does training with one interpolation differ from converting an RF trained with another interpolation? Does post-training conversion between models degrade performance?

It turns out that choosing a different affine interpolation during training is equivalent to changing the time-weighting in the loss function and applying an affine transform to the model parameterization. As long as the transformations $\omega_t$ and $\tau_t$ are not highly singular, converting a model from one affine interpolation to another may not impact the performance dramatically.

Consider a model $v_t(x; \theta)$ trained to approximate the RF velocity $v_t$ of interpolation $X_t = \alpha_t X_1 + \beta_t X_0$ by minimizing a time-weighted mean square loss:

\[\mathcal L(\theta) = \int_0^1 \mathbb E\left[ \eta_t \left \| \dot X_t - v_t(X_t;\theta)\right\|^2 \right] \mathrm dt,\tag{4}\]

where $\eta_t$ is a positive time-weighting function.

After training, we can convert this model $v_t(x; \theta)$ into an approximation $v'_t(x; \theta)$ of $v'_t$ of a different interpolation $X'_t = \alpha_t' X_1 + \beta_t' X_0$ via:

\[v'_t(x; \theta) = \frac{\dot{\tau}_t}{\omega_t} v_{\tau_t}(\omega_t x; \theta) - \frac{\dot{\omega}_t}{\omega_t} x.\]

On the other hand, if we were to train $v'_t(x; \theta)$ directly to approximate the velocity $v'_t$ of interpolation $X'_t = \alpha'_t X_1 + \beta'_t X_0$, the loss function is:

\[\mathcal L'(\theta) = \int_0^1 \mathbb{E} \left[ \eta'_t \left\| \dot{X}'_t - v'_t(X'_t; \theta) \right\|^2 \right] \mathrm dt \tag{5}\]

Matching the loss $(4)$ and $(5)$, shows that the two training schemes differ only in time-weighting and parameterization. Specifically,

\[\eta'_t = \frac{\omega_t^2}{\dot{\tau}_t} \eta_{\tau_t}, \quad v'_t(x; \theta) = \frac{\dot{\tau}_t}{\omega_t} v_{\tau_t}(\omega_t x; \theta) - \frac{\dot{\omega}_t}{\omega_t} x. \tag{6}\]

In other words, training under different affine interpolation schemes is equivalent to applying a different time-weighting function and a corresponding model reparameterization.

Example 2. Loss from Straight to Affine

Consider the straight interpolation $X_t = t X_1 + (1 - t) X_0$ and another affine interpolation $X_t' = \alpha_t' X_1 + \beta_t' X_0.$

Suppose we have trained a model $v_t(x, \theta)$ for the straight interpolation with time weights $\eta_t.$ Then converted $v_t'(x, \theta)$ corresponds to the RF trained with the parametrization in $(6)$, and a different time-weighting:
\[\eta_t' = \frac{\omega_t^2}{\tau_t'} \eta_{\tau_t} = \frac{1}{\dot{\alpha}_t' \beta_t' - \alpha_t' \dot{\beta}_t'} \eta_{\tau_t}.\]
Here, we substitute the relationships derived in Example 1 into $(6)$.

Straight vs. Spherical: Identical Training Loss With Uniform Weights

Following Example 2, an interesting case arises when $\dot{\alpha}'_t \beta'_t - \alpha'_t \dot{\beta}'_t$ is constant, in which case $\eta'_t$ is proportional to $\eta_{\tau_t}$. Furthermore, if $\eta_t = 1$ is uniform, then $\eta'_t$ is also uniform, which implies the two interpolation schemes share the same loss function in this case.

Example 3. Losses for Straight vs. Spherical Interpolation

Consider the spherical interpolation: $X'_t = \sin\left(\frac{\pi t}{2}\right)X_1 + \cos\left(\frac{\pi t}{2}\right)X_0.$

For this choice, $\dot{\alpha}'_t \beta'_t - \alpha'_t \dot{\beta}'_t = \frac{\pi}{2}$. Hence:
\[\eta'_t = \frac{2}{\pi}\eta_{\tau_t}, \quad \tau_t = \frac{\tan\left(\frac{\pi t}{2}\right)}{\tan\left(\frac{\pi t}{2}\right)+1}.\]
Thus, training $v_t(x,\theta)$ for the straight interpolation with a uniform weight ($\eta_t=1$) is equivalent to training $v'_t(x, \theta)$ for the spherical interpolation also with a uniform weight ($\eta'_t=2/\pi$). In this case, the only difference in training for these two interpolations is the reparameterization of the model:
\[v'_t(x, \theta) = \frac{\pi \omega_t}{2} \left( v_{\tau_t}(\omega_t x; \theta) + \left( \cos\left(\frac{\pi t}{2}\right) - \sin\left(\frac{\pi t}{2}\right) \right) x \right),\]
where $\omega_t = (\sin(\frac{\pi t}{2}) + \cos(\frac{\pi t}{2}))^{-1}$ is bounded within $[1/\sqrt{2}, 1]$.

This reparameterization is quite “minor” and does not seem to impact model quality significantly. As shown Figure 5 below, training with straight or spherical interpolation and uniform loss weighting produces nearly identical results.

Figure 6. Training the RF with straight and spherical interpolations using uniform weights yields similar results. The blue curve represents the RF trained with spherical interpolation, while the red curve represents the RF trained with straight interpolation and then converted to spherical interpolation. Since both share the same loss function, as shown in Example 3, the only difference lies in model parameterization, which appears to have limited impact on performance in this case.